When planning to build a small observatory for my imaging gear, my aim was to make it as small as possible in order to save cost and also to make it easy to build and maintain. There are a number of rough guides to building small observatories on the web, but one key consideration seems to be glossed over in all of them. That is how to determine the space needed for the scope and German Equatorial Mount (GEM) to operate without colliding with the floor, walls or roof of the observatory.
As we will see, the calculations are relatively straightforward, but the slightly counter-intuitive nature of GEMs makes it less than obvious to figure them out from first principles. Following this guide, you can work it all out with a tape measure, paper and pencil and some string in a couple of minutes flat.
Our Objective
What we want to know when designing our observatory is how far will the furthest piece of equipment on the mount will reach in any given orientation. If you are building a full-sized observatory, this is not a critical issue. Since you will want to leave plenty of space for the observer(s) to move around the scope, you may just decide to make the observatory ‘big enough’ and leave a lot of extra space around the mount.
In my case I am aiming to build an observatory purely for imaging purposes. I will operate it remotely and so I want to make it as small as physically possible whilst leaving sufficient room for the equipment. The pier will be cast from concrete and so I need to get things right first time.
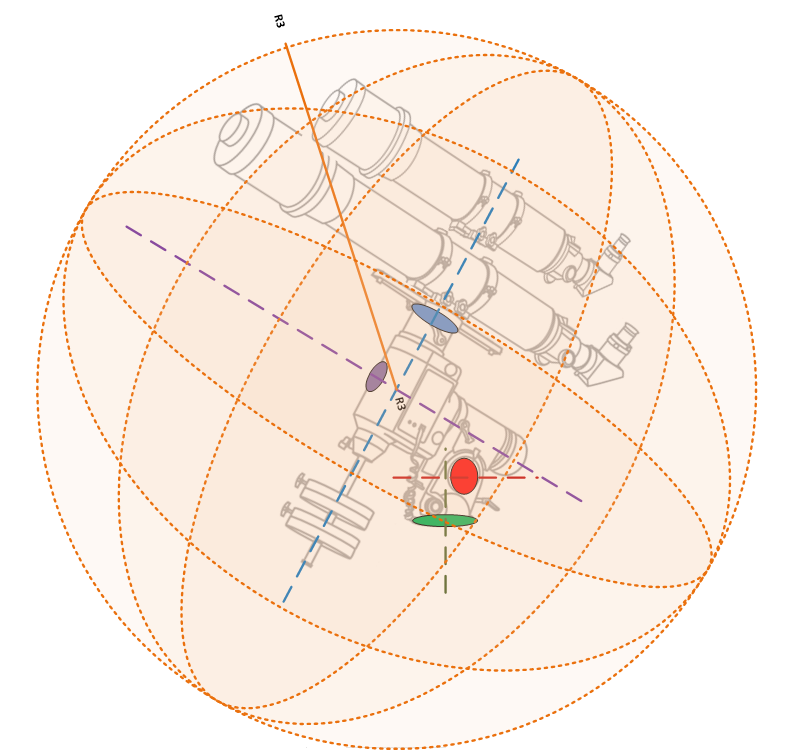
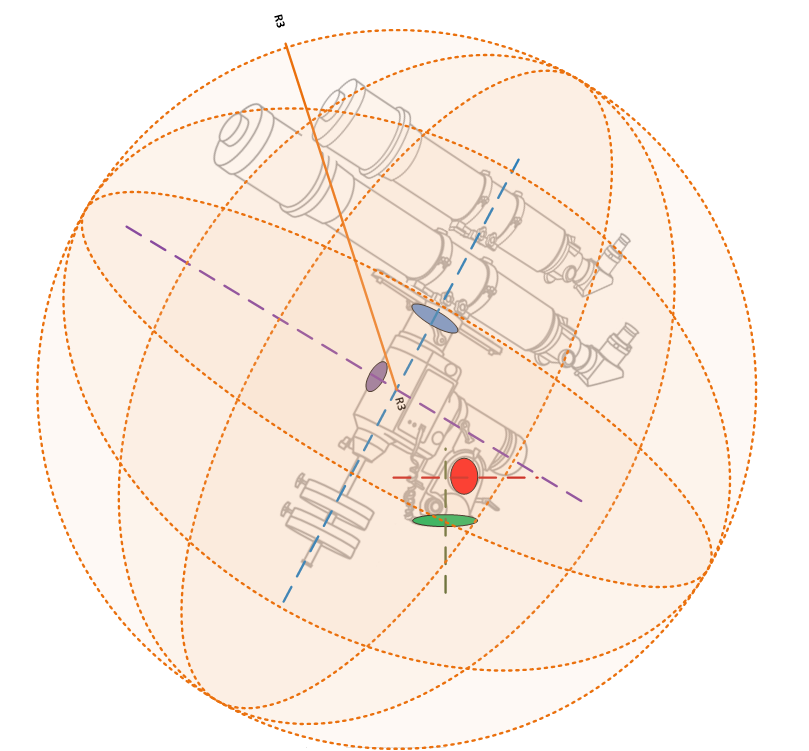
As you no doubt realise, a GEM points the telescope by rotating it around two axes; the Right Ascension Axis (RA), shown in purple in the diagram, and the Declination Axis (Dec) shown in blue.
This means that the telescope has two degrees of freedom (movement around the RA axis and movement around the Dec Axis). The furthest point our equipment can reach must lie on the surface of a sphere with its centre where these two axes intersect (the meeting point of the blue and purple dashed lines above).
This is common sense of course, since the purpose of the mount is to track stars as they move across the celestial sphere. That said, the furthest point our equipment reaches is not necessarily the front of the scope!
Measuring Up
So what we need to do is measure the distance to the furthest point that the equipment can reach. There are two ways to do this. The conservative way is to take two measurements and then do a bit of Pythagoras:
- Firstly, ensure that the polar alignment altitude is set to roughly the correct position for your latitude, as this will affect the height of the observatory.
- Now, as shown in the diagram, we first measure R1 from the centre of rotation of the Dec axis to the furthest point along the OTA. You can easily find the centre of rotation by extending a line up the counterweight shaft. In this case the longest distance along the OTA is from the Dec axis to the front of the main OTA as shown above. Bear in mind that in many cases the longest distance might actually be from the Dec axis back to the rear of the camera cables or eyepiece instead. Measure both in both directions and take whichever is the longest value.
- Next measure R2 from the centre of rotation of the RA axis to the furthest point on the OTA. The centre of rotation can be found by extending a line through the polar scope on most mounts. In this case the furthest point away is the top of the guide scope. Ignore the counterweight bar for now, this is a special case we will deal with below.
- Now you can calculate the furthest distance (the orange line – R3) as follows:
- R3 = √ (R1² + R2²)
- This is just Pythagoras’ theorem if you’ve been out of school for a long time!
- The other method is to directly measure R3 using a piece of string. Hold one end of the string on to the side of the mount immediately above the intersection of the RA and Dec axes and then just sweep the string in a circle (keeping the sweep parallel to the side of the mount). Use your other hand to find the point which is furthest away on the scopes.
As you can probably see, if you have a piggy-back set-up you may end up with a slightly smaller measurement using this method, and it will be at the front of one of the OTAs or back of one of the cameras. If you have a single OTA, the value for R3 should be the same as for the Pythagorean method above. Again it will usually be at the front of the OTA or the back of the camera.
For a side-by-side set-up the string method is much better than the Pythagorean method above. Instead of measuring in a flat plane though, you’re going to have to measure in three dimensions and exercise a bit more judgement. You need to measure the furthest distance between the centre of the mount (where the axes cross) to the most distant ‘corner’ of your side-by-side rig. Since you can’t put your hand in the middle of solid metal you’ll have to measure from one side of the mount or the other (as shown above) but stretch the string out to the four ‘corners’ of the side by side rig, i.e. the furthest point on the front of each OTA, and the furthest point on each of the cameras.
Once you have found the longest distance, add a few extra cm to the value of R3 to account for the fact that you didn’t start the measurement in the middle of the mount, but instead off to one of the sides.

Final Reckoning
Now we have a value for R3, we know the maximum extents the scope can reach is a sphere centred on the intersection of the two axes with a radius of R3. To transfer this to your observatory plans, you just need to draw a circle with a radius of R3 that is centred on the intersection of the mount RA and Dec axes. This will work for both plan and elevation views. Anything on the plan that protrudes in to the circle has the potential to collide with the OTA.*
In the first example we can be confident that the set-up in the first example won’t collide with the walls or roof (in elevation at least, we’d need also need to check in plan view). You can also see the minimum pier height required to avoid collision with the floor. This is the set up I went for in my imaging observatory, but it is likely to be far too low for comfortable visual observing.

In the second example a much longer pier is used. You can see that the OTA will protrude through the left hand (sliding) roof section, but it will not collide with the fixed section on the right. Of course in this case we would need to park the OTA below the roof line in order to close it safely.
* There is always one thing that must protrude in to the circle and that is the pier (or tripod). Hopefully your mount handset or control software has the ability to set mount limits to prevent slewing or tracking the mount in to this necessary but immovable object.
Counterweight Complications
As I hinted above, dealing with the counterweight shaft and weights is a special case. Whilst you are measuring R1, you should also measure the distance from the intersection of the axes to the end of the counterweight shaft, which we will call R4, and the diameter of the counterweights, R5:
- If the R4 is shorter than R1, you can just forget about the counterweights as they will always stay inside the maximum extents that we determined above.
- If the R4 is longer than R1 then you have two choices for dealing with the counterweights.
- The first choice (the easy one) is to use R4 in place of R1 to find the maximum extents sphere as described above. You will end up with more space than you actually need in some directions, but you can be certain that everything will fit in to the observatory with no collisions.
- The other choice is to calculate a cylinder which describes the movement of the counterweights around the RA axis. They describe a cylinder since the counterweights have one degree of freedom.** The radius of the cylinder will be R4, the length will be R5 and the flat surfaces of cylinder will be perpendicular to the RA axis.
- You’ll end up with something that looks a bit like the figure below, with the blue sphere being the OTA extents, and the purple cylinder being the counterweight extents. I’ll leave it as an exercise for the reader to figure out how to translate that in to plan and elevation views. If you find that too difficult, shorten the counterweight bar and use heavier weights to make R4 less than R1!
 ** Technically the counterweights have three degrees of freedom. Since most counterweights are cylindrical (i.e. they have rotational symmetry) and the second degree of freedom is also rotation about the counterweight shaft, we can ignore it. The third degree of freedom is translation (moving the weights up or down the shaft). Using the method described above, you can be sure there is space for the counterweights regardless of where they are along the shaft. If you have a 3D counterweight system of some sort (unlikely for an equatorial mount), then you should treat it as you would the side-by-side rig above find the furthest extent to which it can reach.
** Technically the counterweights have three degrees of freedom. Since most counterweights are cylindrical (i.e. they have rotational symmetry) and the second degree of freedom is also rotation about the counterweight shaft, we can ignore it. The third degree of freedom is translation (moving the weights up or down the shaft). Using the method described above, you can be sure there is space for the counterweights regardless of where they are along the shaft. If you have a 3D counterweight system of some sort (unlikely for an equatorial mount), then you should treat it as you would the side-by-side rig above find the furthest extent to which it can reach.
Other Considerations
There are a few other considerations to bear in mind:
- I said there are only two degrees of freedom to consider for the OTAs, but there are in fact three (I lied, so get over it!) When balancing the telescope OTAs, you might slide them backwards and forwards in the tube rings or adjust the position of the dovetail in the clamp. This is an additional degree of freedom (translation) that you should take in to account when determining R3. You need to figure out the furthest forward (or back) the scope might ever be depending on your balancing needs before you take the measurements.
- The same net effect might occur if you change the length of the imaging train by adding filter wheels, OAGs, spacers, etc. or simply when focusing. Measure R3 for the longest imaging train you plan to use. Of course if you use multiple scopes on the same mount, you need to measure for the longest one.
Advanced Space Saving
There are some final wrinkles if you really need to save some space:
- Firstly, if the furthest point of R3 is at the front of the OTA, it can only reach the lower hemisphere by pointing below the horizon, which won’t make for very exciting images unless you are a fan of shoes. Thus if the rear half of the OTA/camera train (behind the Dec axis) is significantly shorter than the front half, you could use a shorter pier than would be suggested by the measurement of R3. This might be the case if you have a Newtonian, RC or SCT with a heavy mirror at the rear as it will tend to be much further forward in order to balance.
- Thus you can calculate a second version of the maximum extents sphere using a value of R3 based on the distance to the rear of the scope. Combine the larger (upper) hemisphere and the smaller (lower) hemisphere to determine how much space is needed above and below the mount.
- Bear in mind that expensive scope-to-floor or wall collisions would be possible such a scenario, so please ensure that appropriate mount limits are set to avoid the front of the OTA slewing in to the ground or walls. You should also check if there are any special scenarios where the OTA might point below the horizon. The mount’s meridian-flipping strategy should be checked, as should polar-alignment routines (e.g. EQMOD can slew to a ‘weights up’ position when polar aligning).
- If you need to use the polar scope to get your new observatory aligned, don’t make the pier so short as to be unable to see through it (though for an imaging observatory you might have to lie on the floor to do so). Of course you can use a camera and one of the many polar alignment software tools instead.

- Secondly, there may be some directions in which you won’t point the scope below a certain elevation due to obstructions (houses, fences, trees, etc.) or just because of poor quality sky. You might be able to trim some additional space off your observatory by careful planning. For example this arrangement uses a combination of higher pointing and a shorter rear half of the OTA to get the pier much closer to the left hand wall. We could then bring the right hand wall in a lot further (assuming the whole roof slid off instead of the split roof shown):
- Again the approach is to make two sets of maximum extents, one for the value of R3 to the front of the OTAs, and one for value to the rear. This is a more advanced strategy as the risk of collisions is much higher if you get your planning wrong or if the mount moves in an unexpected way and exceeds the limits you have set.
- The main concern is whether the mount will intrude on this ‘forbidden space’ when flipping, parking or other abnormal operations. You’d be well advised to make a mock observatory out of cardboard and perform thorough testing before you proceed to the real build, or just play it safe and make everything large enough to avoid possible collisions.
In the rest of this series of posts, I’ll explain how I went about building the observatory.